이 글은 동적 계획법으로 풀 수 있는 유명한 알고리즘 문제인 최장 증가 부분 수열 문제와 이를 푸는 알고리즘 두 가지에 대해 설명한다.

최장 증가 부분 수열 문제
어떤 임의의 수열이 주어질 때, 이 수열에서 몇 개의 수를 제거해서 부분 수열을 만들 수 있다. 주어진 수열에서 얻을 수 있는 증가 부분 수열 중 가장 긴 것을 찾는 문제를 최대 증가 부분 수열 찾기 문제(LIS: Least Increasing Subsequence)라고 부르며, 이는 매우 유명한 동적 계획법 알고리즘 문제 중 하나이다. 이 문제를 푸는 대표적인 알고리즘이 두 가지 존재한다.
알고리즘
답을 구하는 데에 필요한 배열 A, D를 정의하자. A[i], D[i]는 다음과 같다.
- A[i]: 수열의 i번째 수
- D[i]: A[i]를 마지막 값으로 가지는 가장 긴 증가 부분 수열의 길이
D[i] = (A[i]가 뒤에 추가될 수 있는 가장 긴 증가 부분 수열의 길이) + 1이다.
수열 A = 3 5 7 9 2 1 4 8을 예로 들어 LIS와 그 길이를 구하는 알고리즘 두 가지를 살펴보자.
방법 1
첫 번째 방법은 i=0부터 D[i]를 계산하는데, 각각의 D[i]를 계산할 때마다 앞에 위치한 수들을 모두 확인하여 자신보다 작은 숫자들의 D값 중 최댓값을 찾고 1을 더해 D[i]를 계산한다.
배열 A에 수열을 다음과 같이 저장한다. 알고리즘의 규칙성을 위해 A[0]을 0으로 설정한다. A[0]은 수열에 포함된 수가 아니므로 D[0]=0이다.

i=1) A[1]=3이다. 3은 A[0] 뒤에 붙을 수 있다. 따라서 D[1] = D[0]+1 = 1이다.

i=2) A[2]=5이다. 5는 A[0], A[1] 뒤에 붙을 수 있다. D[0], D[1] 중 D[1]=1이 가장 크므로 D[2] = D[1]+1 = 2이다.
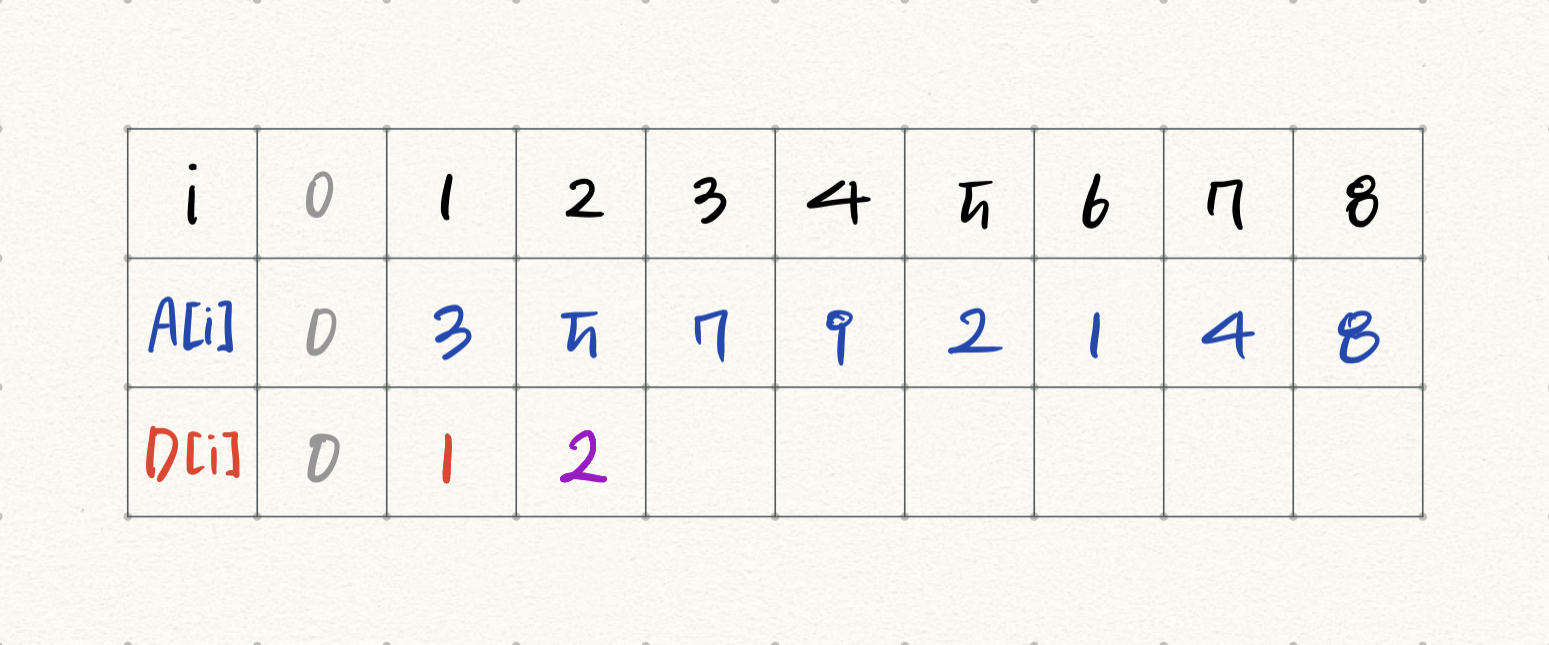
i=3) A[3]=7이다. 7은 A[0], A[1], A[2] 뒤에 붙을 수 있다. D[0], D[1], D[2] 중 D[2]=2가 가장 크므로 D[3] = D[2]+1 = 3이다.

i=4) A[4]=9이다. 9는 A[0], A[1], A[2], A[3] 뒤에 붙을 수 있다. D[0], D[1], D[2], D[3] 중 D[3]=3이 가장 크므로 D[4] = D[3]+1 = 4이다.

i=5) A[5]=2이다. 2는 A[0] 뒤에 붙을 수 있다. 따라서 D[5] = D[0]+1 = 1이다.
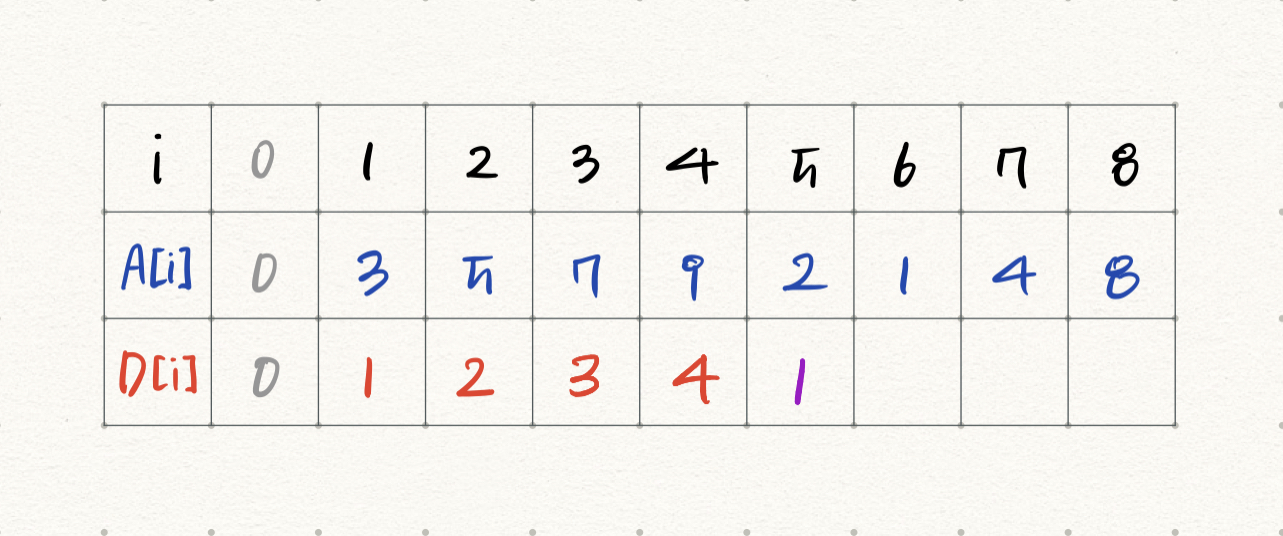
i=6) A[6]=1이다. 1은 A[0] 뒤에 붙을 수 있다. 따라서 D[6] = D[0]+1 = 1이다.

i=7) A[7]=4이다. 4는 A[0], A[1], A[5] 뒤에 붙을 수 있다. 따라서 D[1] = D[0]+1 = 1이다. D[0]=D[1]=D[5]=1이므로 D[4] = 1+1 = 2이다.

i=8) A[8]=8이다. 8은 A[0], A[1], A[2], A[3], A[5], A[6], A[7] 뒤에 붙을 수 있다. D[0], D[1], D[2], D[3], D[5], D[6], D[7] 중 D[3]=3이 가장 크므로 D[8] = D[3]+1 = 4이다.

배열 D에 값을 다 채우면 그 중 가장 큰 값이 최장 증가 부분 수열의 길이이다. 이 예시에서는 LIS의 길이가 4(=D[4]=D[8])이다.
LIS를 찾는 간단한 방법은, LIS의 길이를 D[i]로 가지는 수부터 앞으로 하나씩 작은 D[i]를 찾아나가는 것이다. 이 예시에서는 3 5 7 9(=A[1] A[2] A[3] A[4]), 3 5 7 8(=A[1] A[2] A[3] A[8])이 LIS에 해당된다.
시간 복잡도
이 알고리즘은 수열을 이루는 N개의 수 모두 자신보다 앞에 있는 수들을 확인해야 하므로 O(N^2) 시간복잡도를 가진다.
방법 2: O(NlogN)
두 번째 방법은 앞에 위치한 수들을 모두 확인하여 D[i]를 계산하는 첫 번째 방법과 달리, 표를 활용한다. i=0부터 D[i]를 계산하면서 표에 D[i] 값과 해당 D값을 가지는 숫자(A[i])들 중 최솟값을 저장, 갱신한다. 표에서 A[i]보다 작은 숫자들의 D값 중 최댓값을 구하고 1을 더해 D[i]를 구할 수 있다.
표 X에도 알고리즘의 규칙성을 위해 A[0]=0, D[0]=0으로 설정한다. 첫 번째 방법과의 비교, 더 나은 이해를 위해 첫 번째 방법에서 대응되는 상황을 표 왼쪽에 첨부하였다.
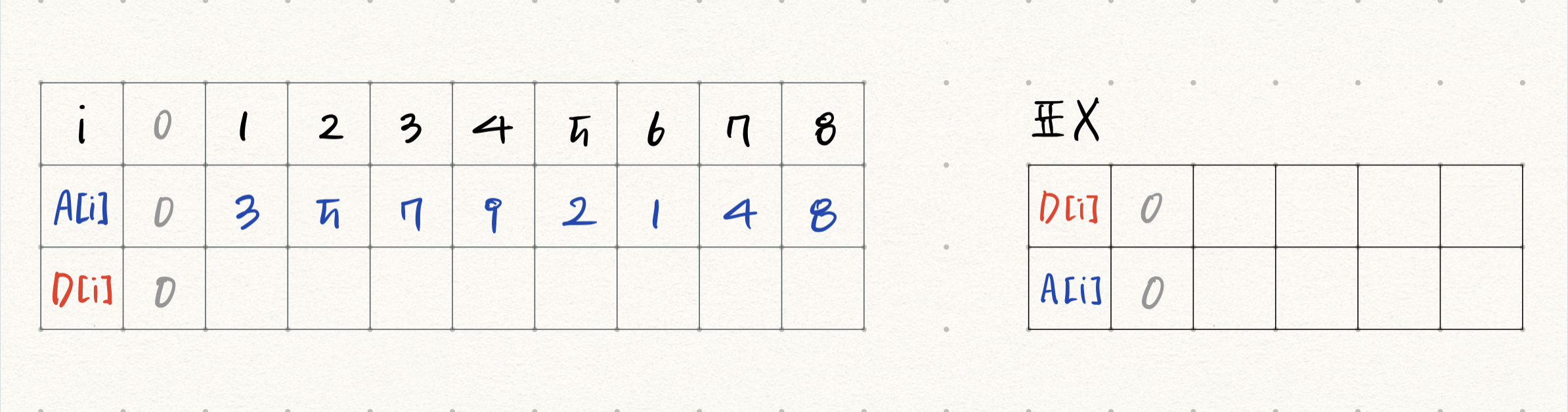
i=1) A[1]=3이다. 표 X에서 3보다 작은 숫자(A[i])들의 D값 중 가장 큰 값은 0이다. 따라서 D[1] = 0+1 = 1이고, 이를 표에 적어준다.

i=2) A[2]=5이다. 표 X에서 5보다 작은 숫자(A[i])들의 D값 중 가장 큰 값은 1이다. 따라서 D[2] = 1+1 = 2이고, 이를 표에 적어준다.

i=3) A[3]=7이다. 표 X에서 7보다 작은 숫자(A[i])들의 D값 중 가장 큰 값은 2이다. 따라서 D[3] = 2+1 = 3이고, 이를 표에 적어준다.

i=4) A[4]=9이다. 표 X에서 9보다 작은 숫자(A[i])들의 D값 중 가장 큰 값은 3이다. 따라서 D[4] = 3+1 = 4이고, 이를 표에 적어준다.

i=5) A[5]=2이다. 표 X에서 2보다 작은 숫자(A[i])들의 D값 중 가장 큰 값은 0이다. 따라서 D[5] = 0+1 = 1이다. 현재 표 X에 D[i]=1인 A 최솟값으로 3이 저장되어있는데, A[5]=2가 더 작으므로 이를 갱신한다.

i=6) A[6]=1이다. 표 X에서 1보다 작은 숫자(A[i])들의 D값 중 가장 큰 값은 0이다. 따라서 D[6] = 0+1 = 1이다. 현재 표 X에 D[i]=1인 A 최솟값으로 2가 저장되어있는데, A[6]=1이 더 작으므로 이를 갱신한다.

i=7) A[7]=4이다. 표 X에서 4보다 작은 숫자(A[i])들의 D값 중 가장 큰 값은 1이다. 따라서 D[7] = 1+1 = 2이다. 현재 표 X에 D[i]=2인 A 최솟값으로 5가 저장되어있는데, A[7]=4가 더 작으므로 이를 갱신한다.
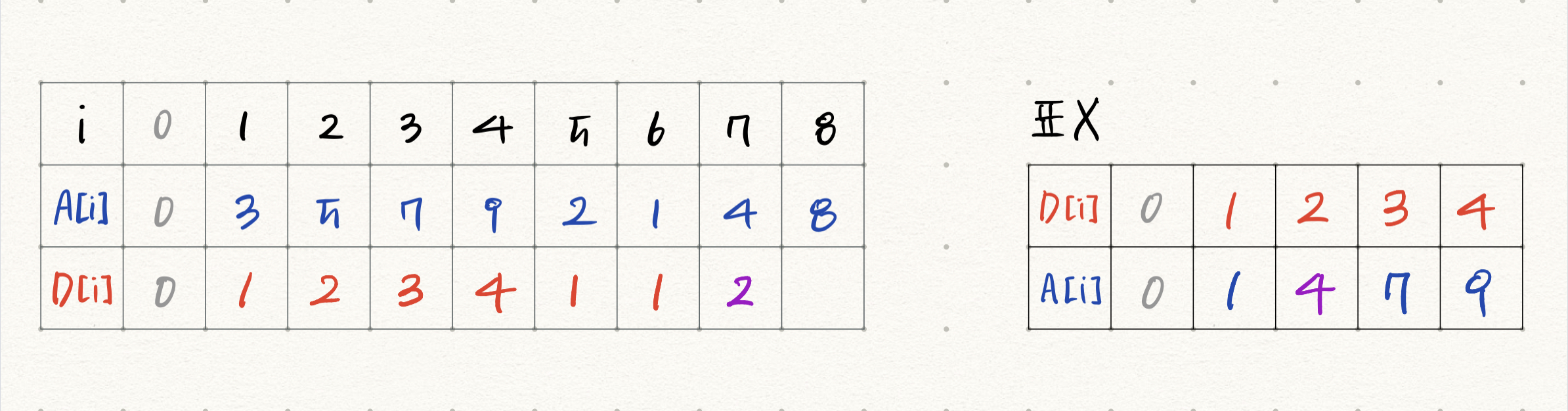
i=8) A[8]=8이다. 표 X에서 8보다 작은 숫자(A[i])들의 D값 중 가장 큰 값은 3이다. 따라서 D[5] = 3+1 = 4이다. 현재 표 X에 D[i]=4인 A 최솟값으로 9가 저장되어있는데, A[8]=8이 더 작으므로 이를 갱신한다.
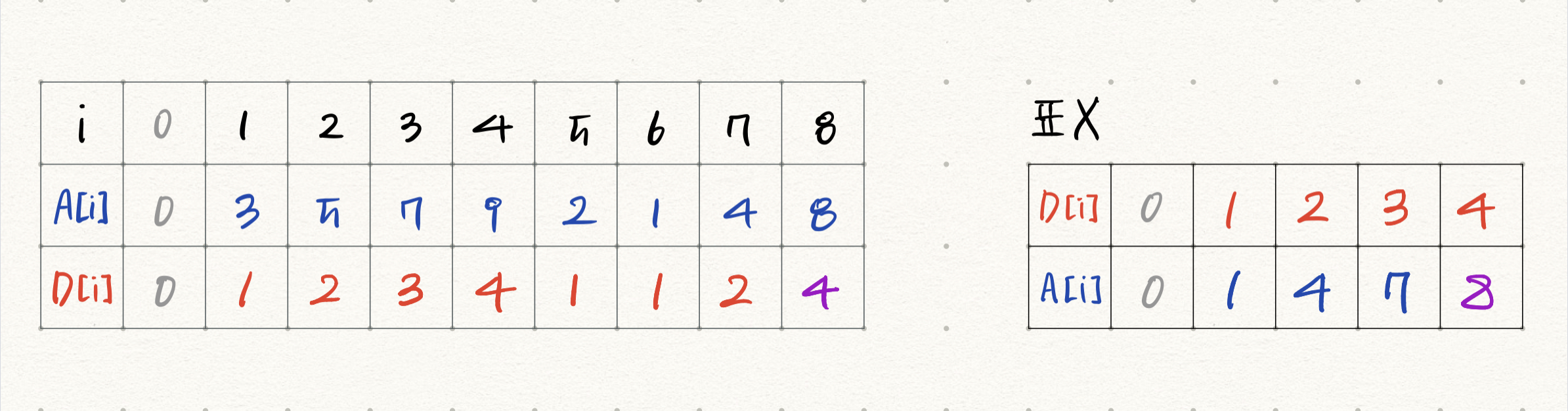
모든 숫자를 검사한 후 표 X의 가장 큰 D값이 LIS의 길이가 된다.
시간 복잡도
이 알고리즘은 N개의 수들에 대해 표 X의 A[i]들을 확인한다. 이때 X는 오름차순으로 항상 정렬되어 있으므로 이진 탐색을 사용할 수 있다. 이진 탐색을 사용하여 현재 A[i]보다 작은 A[i]를 X에서 찾고, 그 A[i]에 해당하는 D값에 1을 더하면 D[i]를 쉽게 구할 수 있다. 따라서 이 알고리즘은 O(NlogN)의 시간복잡도를 가진다.
'Algorithm' 카테고리의 다른 글
| [Algorithm] 백준 14501 퇴사 - node.js (1) | 2021.02.10 |
|---|---|
| [Algorithm] 백준 2839 설탕 배달 - node.js (0) | 2021.02.09 |
| [Algorithm] 백준 5904 Moo 게임 - node.js (0) | 2021.02.06 |
| [Algorithm] 백준 6549 히스토그램에서 가장 큰 직사각형 - node.js (0) | 2021.02.05 |
| [Algorithm] 조합(nCr)의 모든 경우를 구하는 방법(c++, javascript) (0) | 2021.01.30 |



